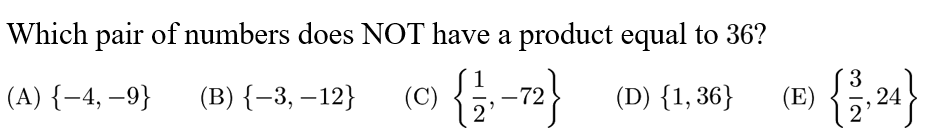
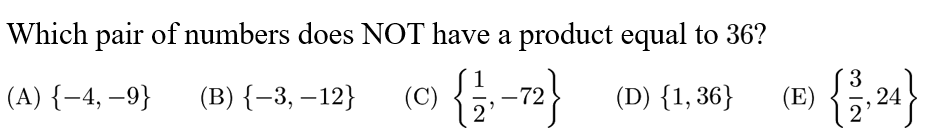
Answer: C
Solution:
C: 1/2 * (-72)=-36.

Answer: C
Solution:
49/84=7/12; 7+12=19.
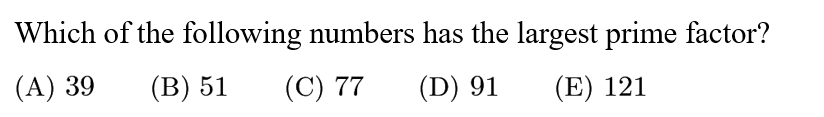
Answer: B
Solution:
A. The largest prime factors of 39 is 13;
B. The largest prime factors of 51 is 17;
C. The largest prime factors of 77 is 11.
D. The largest prime factors of 91 is 13.
E. The largest prime factors of 121 is 11.
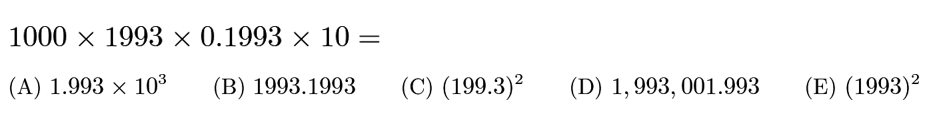
Answer: E
Solution:
=1993*0.1993*1000*10=1993*1993.
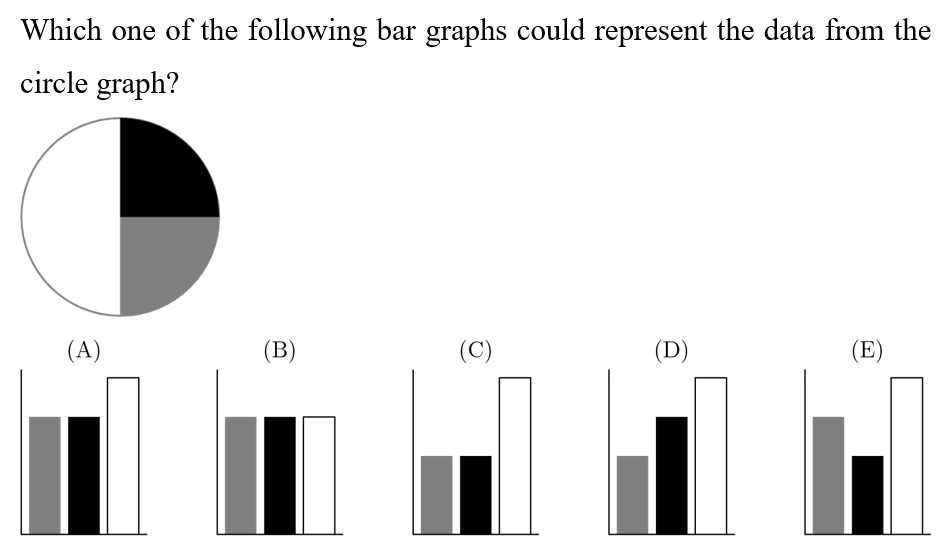
Answer: C
Solution:
Since the white portion of the graph is twice as much as the black and gray, its bar in the bar graph will need to be twice as much as the black and gray. Note that the black and gray portions are equal. This cancels choices A,B, D,E. The final answer is now C.
Answer: B
Solution:
A can of soup will feed 5 children so 15 children are feed by 3 cans of soup. Therefore, there are 5-3=2 cans for adults, so 3*2=6 adults are fed.
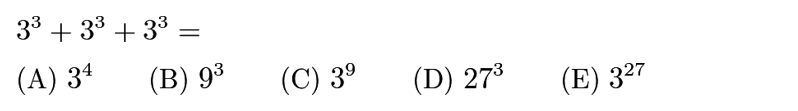
Answer: A
Solution:
=3*3^3=3^4.

Answer: D
Solution:
If Jill's grandmother takes one half of a pill every other day, she takes a pill every 4 days. Since she has 60 pills, the supply will last 60*4=240 days which is about 8 months.

Answer: D
Solution:
Using the chart, (2*4)=3 , (1*3)=3, therefore, 3*3=4.
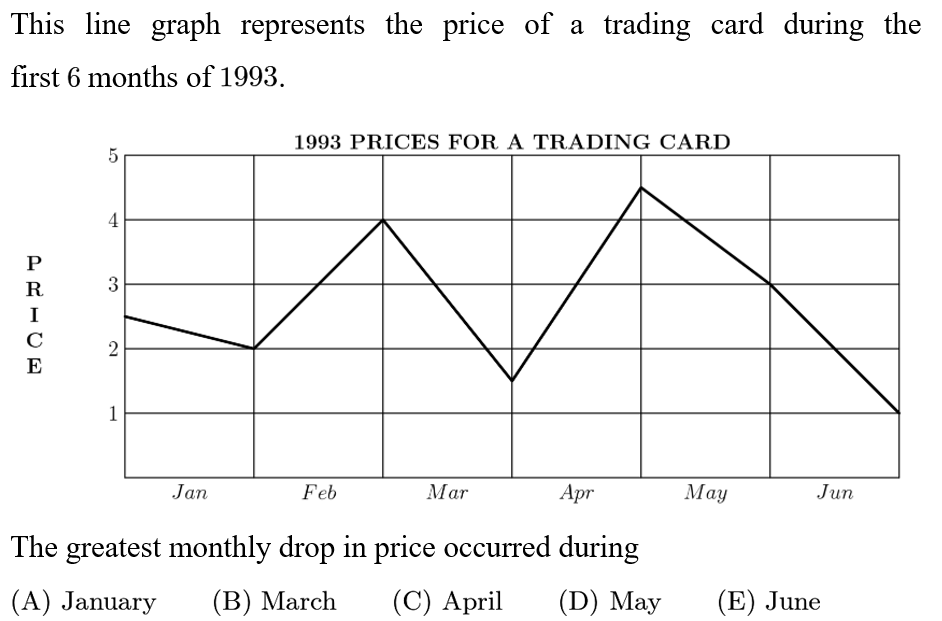
Answer: B
Solution:
The graph shows the following price changes: Jan : Change:-0.50; Feb : Change:+2.00; Mar : Change:-2.50; Apr : Change:+3.00; May : Change:-0.50; Jun : Change:-2.00;
Therefore, March has the largest price drop.


Answer: C
Solution:
Since 81 students took the test, the median is the score of the 41st student. The five rightmost intervals include 2+3+6+12+16=39 students, so the 41st one must lie in the next interval, which is 70.

Answer: E
Solution:
There are a reasonable number of ways to place the operation signs, so guess and check to find that 5-4+6*3=19.

Answer: D
Solution:
Count the number of black squares in each letter. H has 11, E has 11, L has 7, and P has 10, giving the number of black squares to be 11+11+7+10=39. The total number of squares is 15*5=75 and the number of white squares is 75-39=36.

Answer: C
Solution:
B=3, A=1.

Answer: A
Solution:
Say that the four numbers are a, b,c, & 97, then (a+b+c+97) /4 =85. Thus, a+b+c=85*4-87=243, so (a+b+c)/3=81.
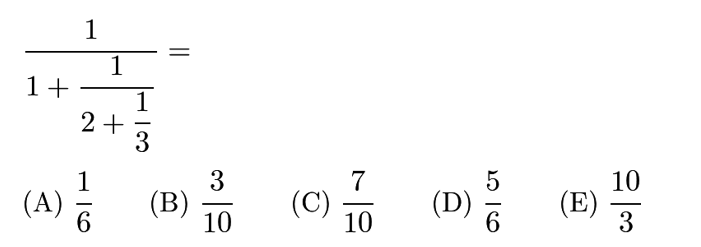
Answer: C
Solution:
=1/(1+1/(2+1/3))=1/(1+1/(7/3))=1/(1+3/7)=1/(10/7)=1*7/10=7/10.
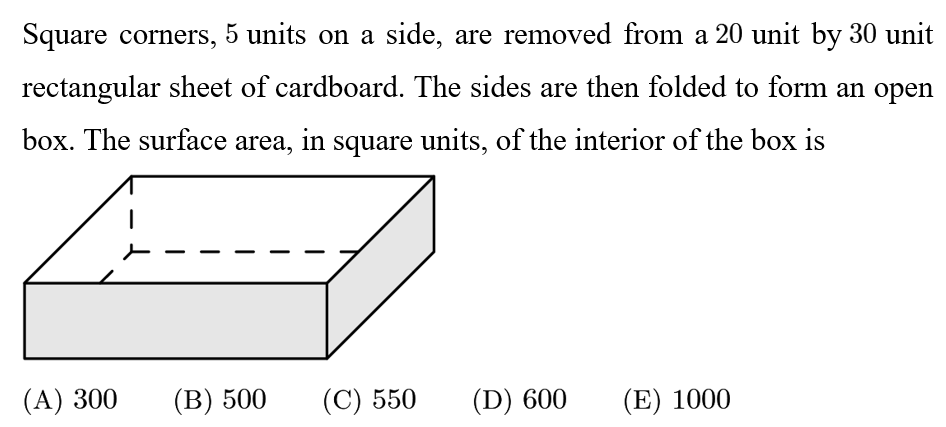
Answer: B
Solution:
If the sides of the open box are folded down so that a flat sheet with four corners cut out remains, then the revealed surface would have the same area as the interior of the box. This is equal to the area of the four corners subtracted from the area of the original sheet, which is 20*30-4*5*5=500.
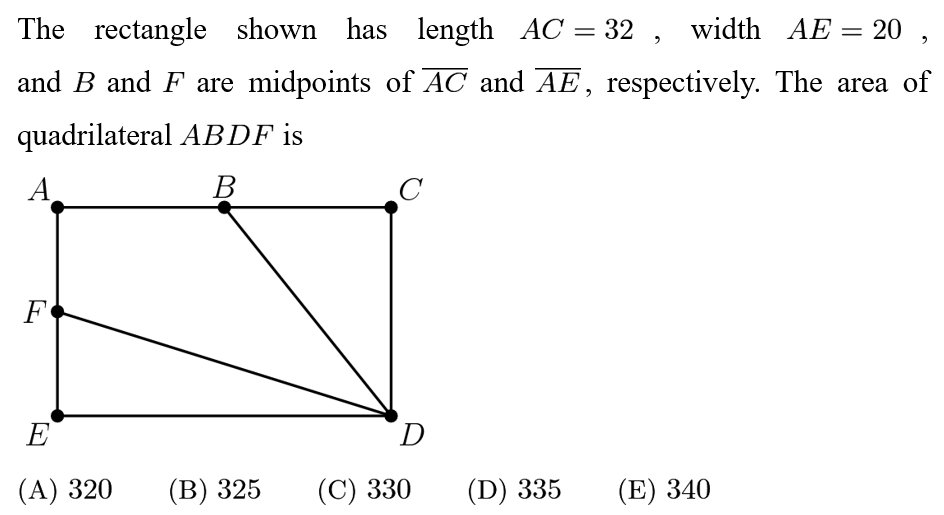
Answer: A
Solution:
The area of the quadrilateral ABDF is equal to the areas of the two right triangles BCD and EFD subtracted from the area of the rectangle ACDE. It’s 20*32-(1/2 * 32*10)-(1/2*16*10)=320.
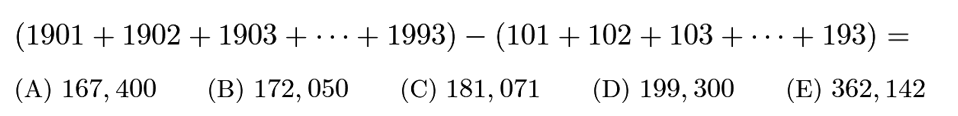
Answer: A
Solution:
=(1901-101)+(1902-102)+(1903-103)+…+(1993-193)=1800+1800+…+1800+1800*93=167,400.

Answer: D
Solution:
100-93=7; 1000-93=907; 10000-93=9907; 100,000-97=99,907,…
10^97-93=9*91+7=826.

Answer: D
Solution:
The area of the new rectangle is : 1.2*L * 1.5*W=1.8*W*L; so it increased 80%.

Answer: D
Solution:
There is 1 two in the one-digit numbers.
The number of two-digit numbers with a two in the tens place is 10 and the number with a two in the ones place is 9. Thus the digit two is used 10+9=10 times for the two digit numbers.
Now, Pat Peano only has 22-1-19=2 remaining twos. The last numbers with a two that he can write are 102 and 112. He can continue numbering the last couple pages without a two until 120, with the last number he writes being 119.

Answer: C
Solution:
First, note that P must beat Q,R,T, and by transitivity, S. Thus P is in first, and not in 3rd. Similarly, S is beaten by P, Q, and by transitivity, T, so S is in fourth or fifth, and not in third.
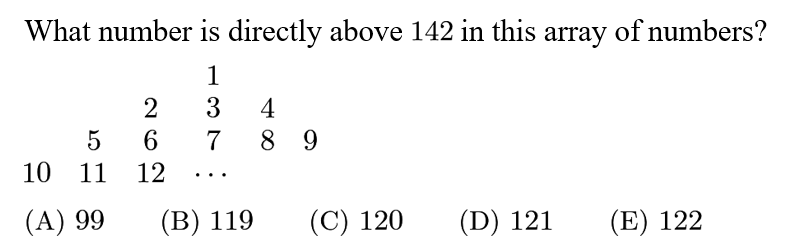
Answer: C
Solution:
Writing a couple more rows, the last number in each row ends in a perfect square. Thus 142 is two left from the last number in its row, 144. One left and one up from 144 is the last number of its row, also a perfect square, and is 121. This is one right and one up from 142, so the number directly above 142 is 120.

Answer: E
Solution:
Using Pythagorean Theorem, the diagonal of the square sqrt((1.5)^2+(1.5)^2)=sqrt(4.5)>2. Because this is longer than 2, the length of the sides of two adjacent squares, the card can be placed like so, covering 12 squares.
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,